One of the most essential functions of Relations and Functions is the Signum Function. It can be explained using a formula in which f(x) represents the signum function. When x is negative, zero, or positive, the signum function returns a value of -1, 0, or 1.
Let’s learn about the signum function, its domain and range, equation, and application in detail for a better understanding of the topic.
What is a Signum Function?
Signum function along with the other types of functions, such as the identity function, rational function, polynomial function, constant function, and the modulus function is an important part of Mathematics.
Mathematically the signum function is defined as:
F(x) = x/|x|, which is also known as the equation of the signum function.
In the above equation,
F(x) represents Signum Function which means that,
F(x) = -1, if x<0
F(x) = 0, if x=0
F(x) = 1, if x>0
In other words, if the value of x is negative, the signum function will be negative (-1), if the value of x is positive, the signum function f(x) will be positive (1), and if the value of x is zero, the signum function will be zero. As a result, the values of x and f (x) are directly proportional to one another.
Click here – Large-Cap Mutual Funds
Domain and range of Signum function
The domain of a real-valued function f (x) is the set of all real numbers for which the expression f (x) can only take real values. In other words, a real-valued function’s domain is the set of all real numbers for which f (x) is meaningful.
The Signum function’s domain is the set R of all real numbers.
A real-valued function’s range is the set of all real values taken by f (x) at places in its domain.
The Signum function’s range is set{-1, 0, 1}.
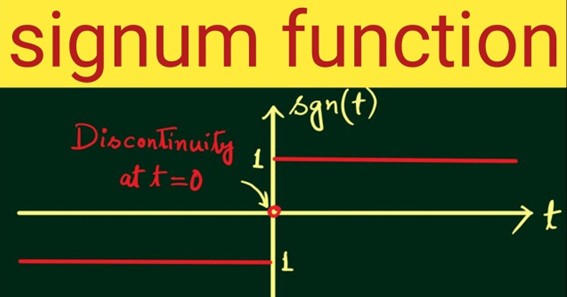
Graph of Signum function
The simplest way to build the graph of any real-valued function is to enter the values of some real numbers into the function and receive their images. When we have both the input and output values, we may plot them on a graph.
Let’s look at a few example sets to plot the graph of the Signum function.
sgn(x)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| sgn(x) | -1 | -1 | -1 | 0 | 1 | 1 | 1 | 1 |
Consequently, the graph of the Signum function appears as follows:
Signum Function for Real Number
The signum function is also known as the derivative of the absolute value function. As a result, each real number has the potential to be expressed as the product of its absolute value. As an example,
x = sgn(x).|x|
As a result, if x is not equal to zero, then
sgn(x) = x/|x|
Applications of Signum Function
The signum function has extensive applications in other areas of mathematics, physics, engineering, and everyday life. The signum function has several useful applications, some of which are listed below.
- The signum function assists in determining the sign of a real number.
- When applied to a complex number, the signum function aids in projecting it on the unit circle.
- The integration of a signum function produces a line that is inclined positively or negatively with respect to the x-axis.
- The use of probability for a signum function forecasts whether or not an event will occur.
- The signum function concept can be seen prominently in any of the on-off function switches. The switches can be set to turn on or off based on the defined input values or variations in the input values.
- The use of the signum function can be seen in a thermostat. Above a specific temperature, the system turns on and begins cooling; below that temperature, the system turns off and ceases cooling.
Click here – How To Find the Best Health Insurance Policy?